Prąd przemienny (AC) – zanim zaczniesz czytać rozdziały w ramach tego działu, upewnij się czy masz opanowane wszystkie zagadnienia z prądu stałego (DC), ponieważ wszystko co zostało tam omówione będzie analogicznie wykorzystywane w zadaniach z prądem przemiennym.
Prąd przemienny – to prąd zmienny, okresowy; charakteryzuje się określoną częstotliwością. Prąd płynie raz w jednym kierunku raz w przeciwnym. Przebieg takiego prądu można opisać przy pomocy wykresu sinusoidalnego.
Sygnał – można zdefiniować w wielkim uproszczeniu jako zobrazowanie zmienności dowolnej wielkości fizycznej – w naszym przypadku będzie to napięcie lub natężenie prądu elektrycznego – opisujemy go między innymi za pomocą funkcji jednej zmiennej – funkcji czasu: f(t).Głównie sygnały wykorzystywane są do przenoszenia lub zbierania informacji.
Wymuszenia sinusoidalne należą do najważniejszych rodzajów sygnałów w teorii obwodów ze względu na to, że codziennie mamy do czynienia z sinusoidalnym napięciem i/lub prądem generowanym w elektrowniach i obecnym w instalacjach elektrycznych w naszych domach.
SYGNAŁY SINUSOIDALNE (przebiegi czasowe)
Napięcie, bądź prąd zmienny można przedstawić za pomocą poniższego wzoru, z użyciem funkcji sinus. Dziedziną tej funkcji jest w tym przypadku czas.

Opis parametrów
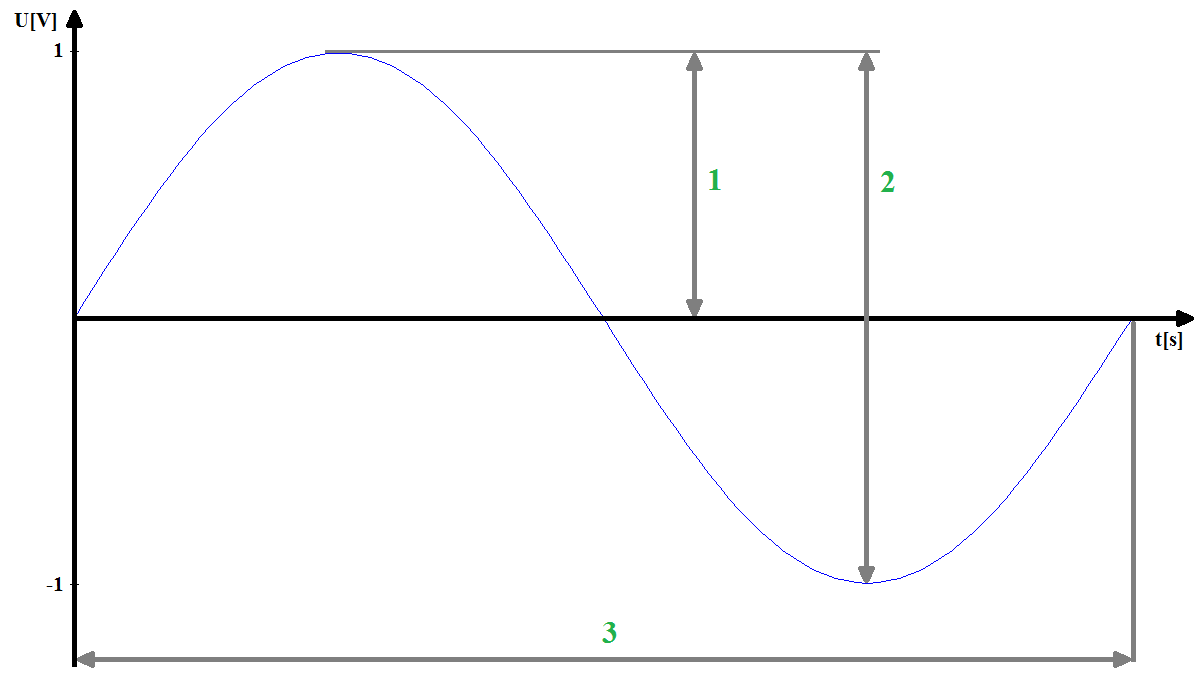
Amplituda [nr 1 na rysunku]
Wartość międzyszczytowa (peak-peak): U_{PP} [nr 2 na rysunku]
Okres [nr 3 na rysunku] : T=\frac{1}{f} [s], gdzie f [Hz] - częstotliwość
Pulsacja: \omega=2 \pi f
Wartość skuteczna: U_{sk}=\sqrt{\frac1T\int_0^Tu^2(t)dt}
( wartość skuteczna prądu AC - jest to taka wartość prądu DC, że podczas jednego okresu powoduje wydzialanie takiej samej mocy co dany sygnał prądu AC. )
Dla sygnału sinusoidalnego można zdefiniować wzór na wartość skuteczną: U_{sk}=\frac{U_{max}}{\sqrt{2}}
Faza początkowa (\varphi_0, \varphi_1) wpływa na wartość funkcji w chwili t=0 i przesuwa wykres względem tej chwili czasu.
Przesunięcie fazowe (\varphi) to różnica położenia jednego przebiegu względem drugiego: \varphi=|\varphi_0-\varphi_1|

Wartość średnia: U_{sred} =\frac1T\int_0^Tu(t)dt
Współczynnik kształtu: K_k=\frac{U_{sk}}{U_{sred}}
(stosunk wartości skutecznej do średniej)
Układy (SLS), które będziemy analizować spełniają poszczególne założenia, mianowicie są:
- Skupione
- Liniowe
- Stacjonarne
BIBO stabilność – występuje w układach SLS jeśli ograniczone pobudzenie systemu, układu daje ograniczoną reakcję.
