Prawa Kirchhoffa

Prawa Kirchhoffa bardzo powszechnie wykorzystuje się do analizy obwodów. Poniżej zaprezentowano definicje, a także przykład oparty na rozwiązaniu zadania z wykorzystaniem tych praw.

Pierwsze Prawo Kirchhoffa (prądowe):

Definicja: Algebraiczna suma prądów wpływających do danego węzła jest równa algebraicznej sumie prądów wypływających z tego węzła.

Jak widać na powyższym rysunku zilustrowano I Prawo Kirchhoffa. Prąd wpływający do węzła jest z „plusem”, natomiast prądy wypływające są z „minusem”. Oczywiście oznaczenia są umowne i równie dobrze można przyjąć je odwrotnie.

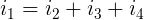
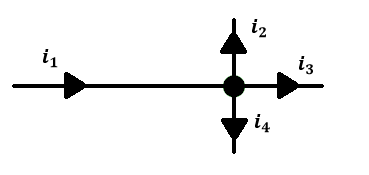
Drugie Prawo Kirchhoffa (napięciowe):

Definicja: W każdym oczku obwodu suma spadków napięć na każdym z elementów jest równa sumie napięć źródeł energii.

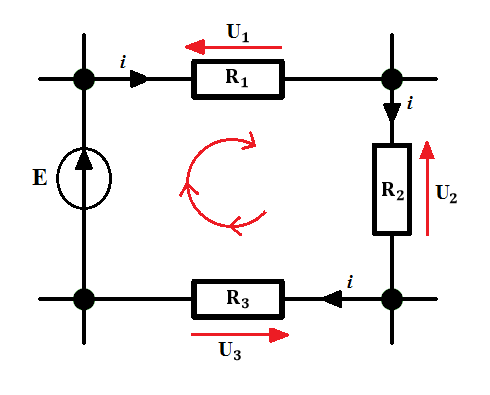
Na rysunku przedstawiono graficznie do czego odnosi się drugie Prawo Kirchhoffa. Widzimy fragment obwodu tj. oczko, które jest zamknięte. Chcąc rozwiązać takie zagadnienie musimy najpierw zaznaczyć spadki napięć na każdym odbiorniku energii. Spadki te występują, ponieważ w oczku jest również źródło napięcia E . Zatem suma wszystkich napięć będzie równa 0. Konieczne jest też zaznaczenie kierunku zgodnie z którym dane napięcie będzie z plusem lub w przeciwnym wypadku z minusem. Równania dla tego oczka są następujące:

Oba te prawa, a także prawo Ohma pozwala nam na tzw. „rozwiązywanie obwodów”

Przykład dla Prawa Kirchhoffa:

(Kliknij tutaj, aby zobaczyć ten przykład w symulatorze)
W zaprezentowanym poniżej obwodzie należy wyliczyć wartość prądu I, I_3 napięcie źródła oraz całkowitą moc obwodu.

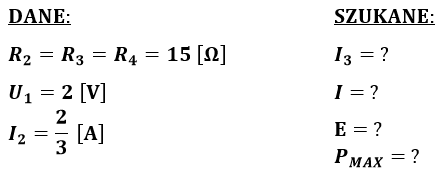
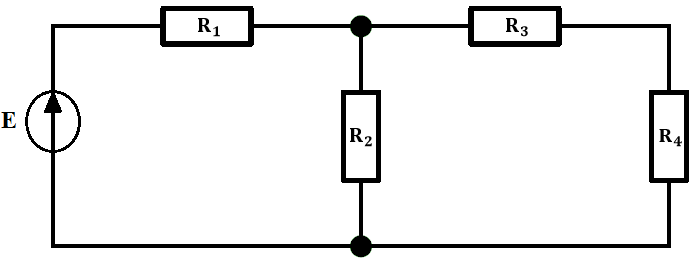
Rozwiązanie:

Mamy obwód składający się z dwóch oczek. Zatem na początku zaznaczymy na schemacie spadki napięć i prądy:
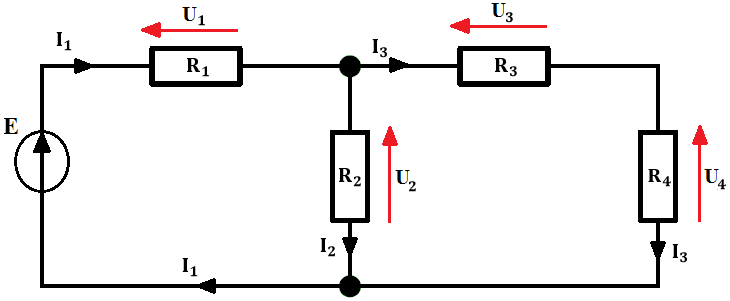
Obliczamy prąd I_3 płynący w gałęzi, w której znajdują się rezystory R_3 i R_4 połączone szeregowo. Zatem, dla uproszczenia obwodu skorzystamy z tego faktu i policzymy rezystancję zastępczą R_{34} . Zaznaczmy kierunki w oczkach – według nich będziemy zapisywać odpowiednie równania wynikające z II prawa Kirchhoffa:

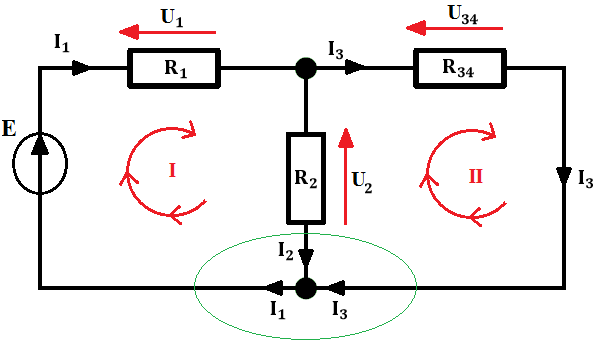
Teraz mając wszystkie wielkości możemy skorzystać z praw Kirchhoffa i prawa Ohma do rozwiązania tego obwodu. Korzystając z drugiego prawa Kirchhoffa napiszmy równanie dla II oczka: U_2 będzie ze znakiem plus, ponieważ spadek napięcia jest zgodny z kierunkiem, który sobie ustaliliśmy. U_{34} będzie z minusem, ponieważ spadek napięcia na tym odbiorniku jest przeciwny do naszego kierunku. Równanie będzie przedstawiać się następująco:

Korzystamy z prawa Ohma (Spadek napięcia na odbiorniku jest równy iloczynowi rezystancji tego elementu i prądu przepływającego przezeń), zatem:

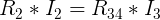
Do obliczenia prądu I_1 skorzystamy z I prawa Kirchhoffa: (prądy I_2 i I_3 będą z plusem, gdyż dopływają do węzła zaznaczonego zielonym kółkiem na rysunku powyżej, a I_1 będzie z minusem, ponieważ wypływa)

Policzymy teraz wartość napięcia źródła E. Do tego celu skorzystamy z II prawa Kirchhoffa dla I oczka naszego obwodu. Zgodnie z zasadami, z których korzystaliśmy wyżej równania są następujące:

Ostatnie co zostało do policzenia to całkowita moc obwodu, którą liczymy ze wzoru:

To wszystko co należało policzyć w powyższym przykładzie. Zachęcam do przeanalizowania go na spokojnie i w celu lepszego utrwalenia materiału zapraszam do działu z zadaniami.

<< Spisu tematów           Tw. Thevenina >>