Twierdzenie Thevenina – zanim zaczniemy należy zapoznać się z zagadnieniem dzielnika napięcia.
Dzielnik Napięcia
Dzielnik Napięcia – najprostszy czwórnik bardzo często wykorzystywany w różnych układach. Główną funkcją – jak nazwa wskazuje – jest „podział” napięcia, czyli zmniejszenie napięcia wyjściowego w stosunku do napięcia wejściowego.
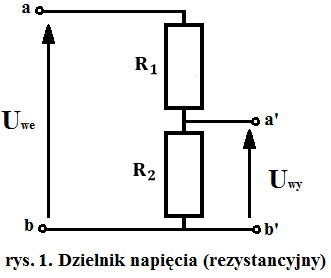Dzielnik napięcia można zbudować także z innych elementów pasywnych tj. cewek i kondensatorów. Jak widzimy na powyższej grafice (rys 1.) między zaciskami a’ i b’ napięcie to nic innego jak spadek napięcia na rezystorze R_2. Spadek ten jest uzależniony od wartości rezystorów R_1 i R_2, a także od obciążenia na wyjściu. Dla nieobciążonego dzielnika wyprowadza się następujący wzór na napięcie wyjściowe:
Przekładnia dzielnika
Przekładnia dzielnika – jest to stosunek napięcia wejściowego do napięcia wyjściowego:
Twierdzenie Thevenina
Każdy liniowy, aktywny obwód elektryczny można przedstawić jako źródło napięcia jałowego między wybranymi zaciskami wyjściowymi i rezystancję zastępczą od strony zacisków, która jest równa rezystancji tego układu po zwarciu wszystkich źródeł napięć.
Aby rozwiać wszelkie wątpliwości rozważmy twierdzenie Thevenina zastosowane w przykładzie.
Przykład Twierdzenie Thevenina
Mamy zadanie, w którym musimy obliczyć spadek napięcia oraz moc wydzielaną na rezystorze R_1, w poniższym układzie. Należy skorzystać z twierdzenia Thevenina. (Symulator obwodu)
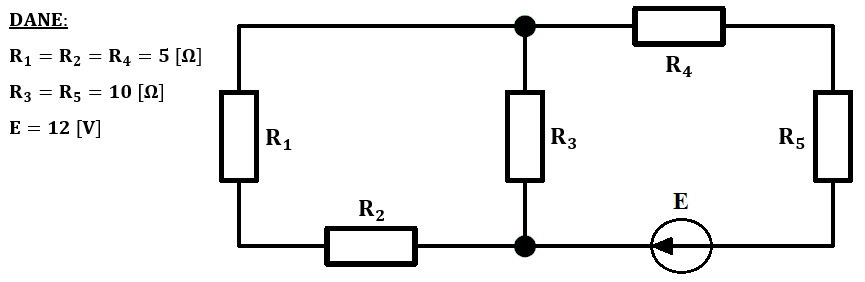
Rozwiązanie
W poleceniu podane jest, że musimy skorzystać z tw. Thevenina. Należy policzyć spadek napięcia i moc wydzielaną na rezystorze R_1. W tym przypadku, korzystając z twierdzenia Thevenina musimy stworzyć obwód zastępczy, który będzie składać się z rezystancji zastępczej i napięcia jałowego od strony zacisków a i b (napięcie jałowe to napięcie panujące na zaciskach a i b bez obciążenia).
W pierwszej kolejności trzeba ustalić gdzie umieścić zaciski a i b. Sprawa jest prosta, a mianowicie ustawiamy sobie zaciski na gałęzi, na której znajduje się badany element.
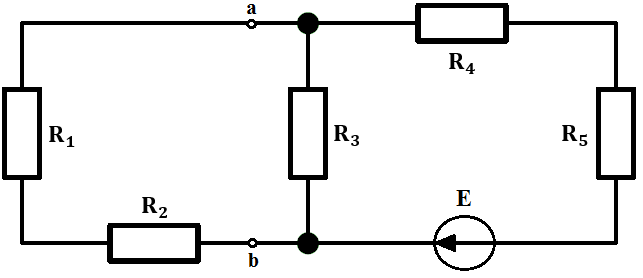
Teraz zrobimy schemat zastępczy zgodnie z twierdzeniem:
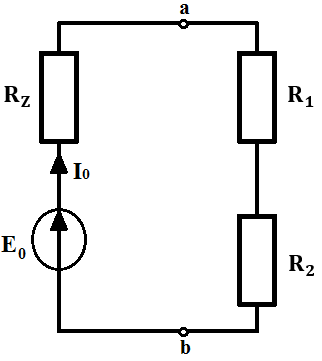
I_0, napięcie w stanie jałowym E_0, rezystancja zastępcza R_z i rezystancje na gałęzi R_1 i R_2.
Aby obliczyć spadek napięcia na R_1 należy skorzystać ze wzoru:
A moc wydzielaną na rezystorze R_1:
Wzór na prąd w tym obwodzie: (Zgodnie z prawem Ohma)
Do policzenia szukanych potrzebujemy znać wartość prądu I_0, którą możemy obliczyć z powyższego wzoru. Potrzebujemy jednak jeszcze znać wartość E_0, a także R_Z.
Zacznijmy od R_Z – zgodnie z twierdzeniem Thevenina źródło napięcia zostanie zwarte, tak więc mamy następującą sytuację:
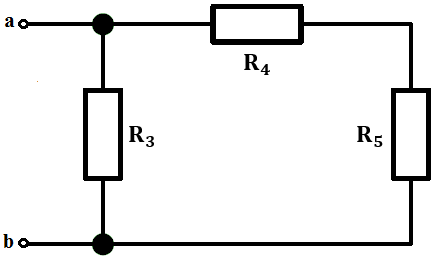
R_4 i R_5 łączymy szeregowo:
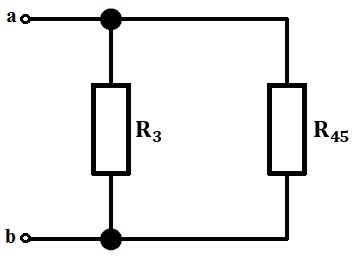
R_3 i R_{45} łączymy równolegle i mamy naszą szukaną rezystancję zastępczą:
Ostatnia nieznana wielkość to E_0, którą teraz policzymy. Napięcie E_0, jest napięciem występującym na zaciskach ab. A dokładniej jest to spadek napięcia na rezystorze R_3 – co bardzo dobrze obrazuje poniższy rysunek:
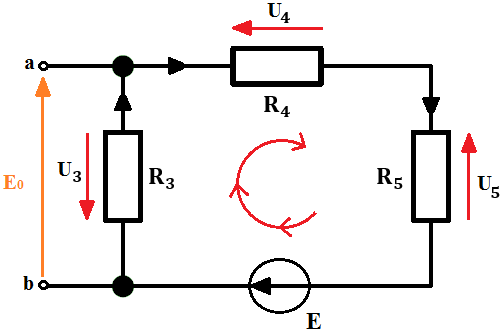
E_0 skorzystamy z praw Kirchhoffa i prawa Ohma, zatem:
* II prawo Kirchhoffa:
* Wchodzi prawo Ohma i zasada superpozycji (suma poszczególnych spadków napięć na odbiornikach i napięcia E jest równa 0):
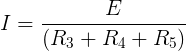
Podstawiając liczby:
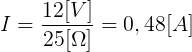
Teraz możemy obliczyć spadek napięcia na R_3, czyli E_0:
Mamy wszystkie potrzebne wartości. Możemy podstawić do naszych wzorów:
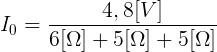
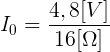
Następnie do wzorów, z których obliczamy wielkości będące ostateczną odpowiedzią:
(Odp. Spadek napięcia wynosi 1,5 V)
(Odp. Moc czynna wydzielona na R_1 wynosi 450 mW)
bardzo fajnie wytlumaczone