Twierdzenie Nortona – zagadnienie, które omówimy, ale na początek należy omówić zagadnienie dzielnika prądu. Jest to połączenie równoległe elementów pasywnych, którego główną funkcją jest zmniejszenie natężenia prądu.
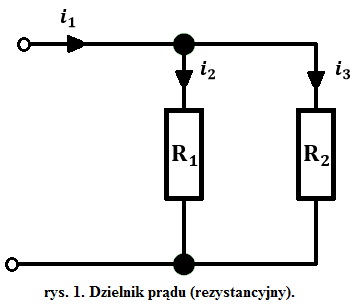
Wzory wynikające z takiego połączenia i odpowiednich praw panujących w obwodzie:
TWIERDZENIE NORTONA:
Drugim zagadnieniem poruszonym w zakresie tego rozdziału będzie twierdzenie Nortona.
Na mocy twierdzenia Nortona możemy przedstawić dowolny układ źródeł prądu/napięcia i innych elementów pasywnych jako układ składający się ze źródła prądowego emitującego prąd zwarcia (po zwarciu gałęzi badanej na zaciskach A-B), a także połączonej równolegle konduktancji zastępczej. Następnie na zaciskach umieszcza się analizowaną gałąź z interesującym nas elementem.
Być może wydaje się to zawiłe, aczkolwiek poniższy przykład powinien rozwiać jakiekolwiek wątpliwości.
Przykład 1. Oblicz moc wydzielaną na rezystorze R_1. Skorzystaj z twierdzenia Nortona.
Tak w ogóle to po co ? Ano, z tego twierdzenia jak i z twierdzenia Thevenina korzysta się jeśli chcemy dowiedzieć się jakie są prądy lub napięcia w jednym ograniczonym fragmencie obwodu, bez analizy całości. Głównie wykorzystuje się to przy bardziej skomplikowanych układach, aczkolwiek ze względu na edukacyjny charakter tego rozdziału przeanalizujemy prosty przykład, aby zrozumieć ideę.
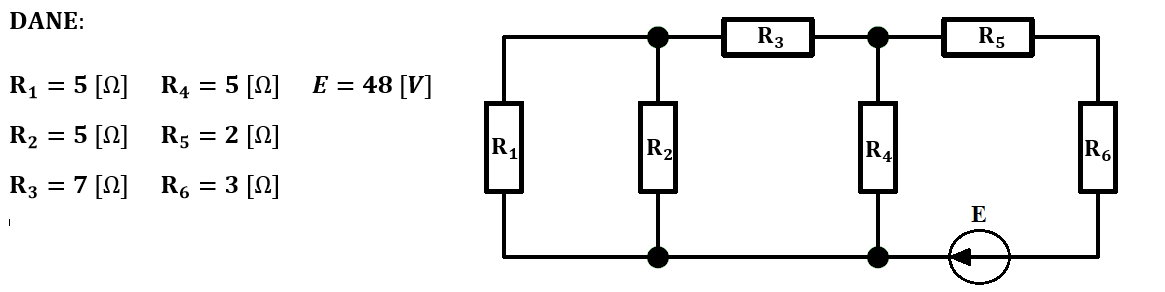
Rozwiązanie:
1. Wstawiamy zaciski na interesującej nas gałęzi, czyli w tym przypadku na gałęzi, na której znajduje się rezystor R_1.
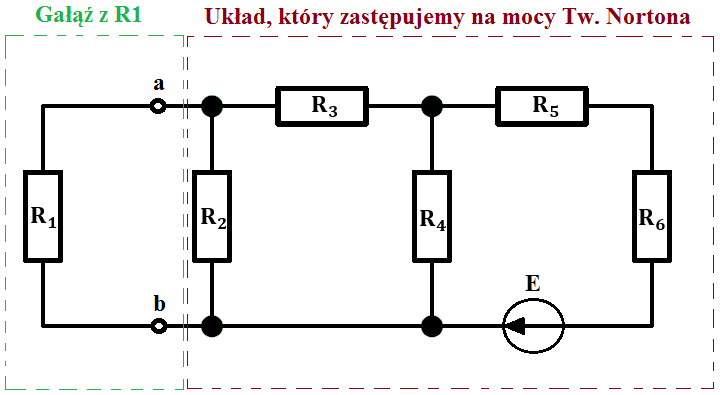
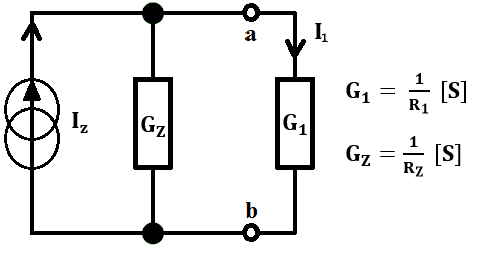
Konduktancja to nic innego jak odwrotność rezystancji, a jednostką jest Siemens – [S].
3. W zadaniu należy wyznaczyć moc wydzielaną na rezystorze R_1, zatem musimy znać prąd I_1. Powyższy układ jest dzielnikiem prądu, zatem skorzystamy z tego faktu.
Musimy tylko znać wartości R_Z i I_{ZW}, które teraz wyliczymy.
Zacznijmy od R_Z – sytuacja jest prosta, w obwodzie jest źródło napięciowe, które zastępujemy zwarciem i wyliczamy rezystancję zastępczą. W przypadku wystąpienia źródła prądowego – zastępujemy je rozwarciem. (Więcej na ten temat w rozdziale 1, a także przy okazji omawiania twierdzenia Thevenina w rozdziale 4).
4. Po wykonaniu obliczeń wynikiem jest:
5. Obliczamy prąd zwarcia. W tym celu zwieramy rezystor R_1, czyli usuwamy go tak jak jest to przedstawione na poniższym rysunku.
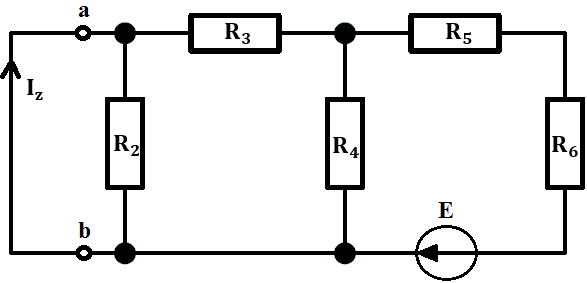
a) usuwamy rezystor R_2 – dlaczego ? – dlatego, że prąd popłynie drogą bez rezystora, bez oporu. Droga ta jest zaznaczona poprzez I_Z na rysunku.
b) połączymy szeregowo rezystory R_4 i R_5.
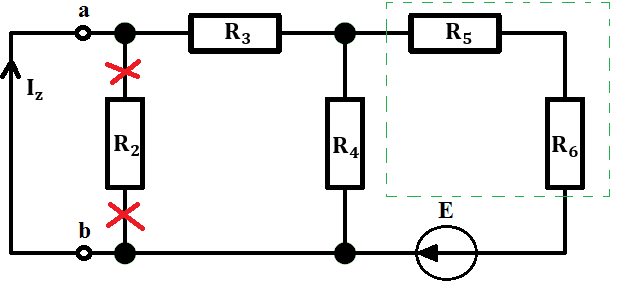
Po uporządkowaniu:
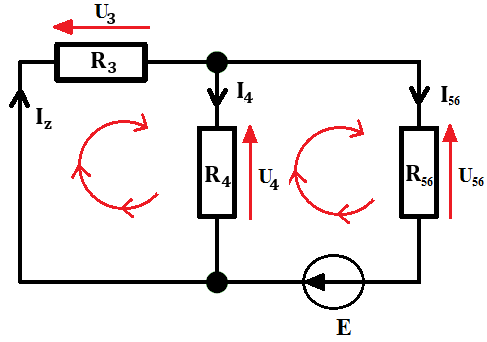
Prosty obwód, w którym możemy wykorzystać Prawa Kirchhoffa i Prawo Ohma, aby rozwiązać go i znaleźć szukane przez nas wartości.
Ułóżmy równania wynikające z tych praw:
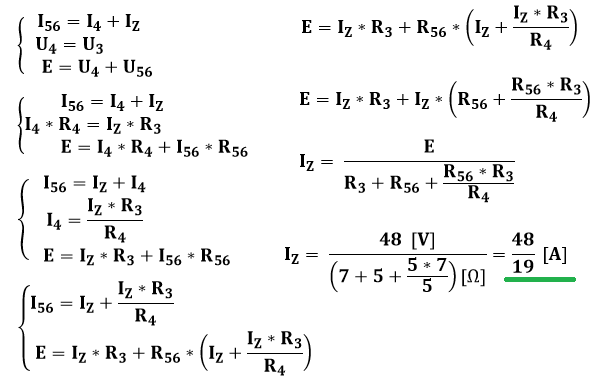
6. Ostateczne rozwiązanie. Mamy wszystkie wielkości, zatem możemy podstawić do wzoru:
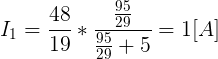Zatem moc wydzielana na rezystorze będzie równa:
(odpowiedź !!!)