Metoda symboliczna upraszcza pod względem obliczeniowym analizę obwodów prądu przemiennego. Główną ideą jest po prostu zamiana przebiegów czasowych na liczby zespolone i operowanie nimi. Stosuje się ją zazwyczaj jeśli interesuje nas stan ustalony w obwodzie i pobudzenia są o tej samej pulsacji.
Dzięki temu uproszczamy obliczenia, które wynikałyby choćby z działań na funkcjach trygonometrycznych co często jest czasochłonne i stosunkowo łatwo można popełnić błąd. Zaczniemy jednak od zdefiniowania impedancji i reaktancji – jest to kluczowe w obwodach prądu AC i niezbędne przy obliczaniach.
Reaktancja – pewnego rodzaju opór. Występuje jeśli w obwodzie jest element pojemnościowy (np. kondensator) i/lub indukcyjny (np. cewka). Jest częścią urojoną impedancji i jeśli wielkość ta jest ujemna to obwód ma charakter pojemnościowy, w przeciwnym wypadku, gdy jest dodatnia to charakter jest indukcyjny.
Impedancja – to również opór, jednak bardzo uogólniony. W zasadzie rezystancja i reaktancja wchodzą w skład impedancji. Można przedstawić ją za pomocą liczby zespolonej, gdzie częścią rzeczywistą (rezystancją) opisany jest opór, w którym płynący prąd jest zgodny w fazie z przyłożonym napięciem, natomiast częścią urojoną (reaktancją) – przesunięcie w fazie.
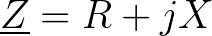
gdzie: X - reaktancja, R - rezystancja, Z - impedancja
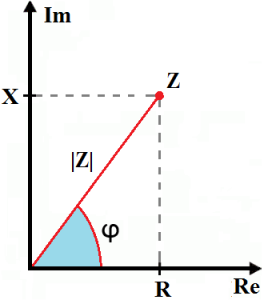
(Aby zrozumieć ten temat i robić przykłady, zadania należy dobrze śmigać z liczbami zespolonymi)
Impedancja rezystora:

Impedancją idealnego rezystora jest część rzeczywista, część urojona jest zerowa.
Impedancja induktora:

Impedancja idealnego induktora jest urojona (przy zerowej części rzeczywistej)
X>0 - charakter indukcyjny
Impedancja kondensatora:

Impedancja idealnego induktora jest urojona (przy zerowej części rzeczywistej)
X<0 - charakter pojemnościowy
METODA SYMBOLICZNA – WYKORZYSTANIE W PRAKTYCE
> Przebieg czasowy napięcia dany jest wzorem:

> Przechodzimy na postać tzw. wartość zespoloną:

Aby przejść należy amplitudę podzielić – w przypadku przebiegu sinusoidalnego – przez \sqrt{2}, natomiast argumentem \varphi jest przesunięcie fazowe, ponieważ czas jest zerowany, więc nie uwzględniamy pulsacji. Zatem wartość zespolona jest niezależna od czasu.
W powrocie do przebiegu czasowego moduł liczby zespolonej mnożymy razy \sqrt{2}, a kąt liczby zespolonej jest brany jako faza przebiegu.
Dzięki takim przekształceniom nie tylko uproszczą nam się obliczenia, ale również będziemy mogli korzystać z metod, które wykorzystywane są w analizie prądu stałego.
Łączenie impedancji: analogicznie jak przy łączeniu rezystancji (przykład 1)
Przykład 1. (metoda symboliczna – impedancja)
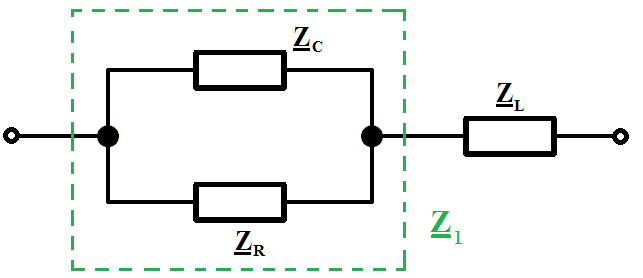
Obliczyć impedancję dwójnika, dla danej pulsacji \omega_0. Wynik przedstawić w postaci algebraicznej i wykładniczej.
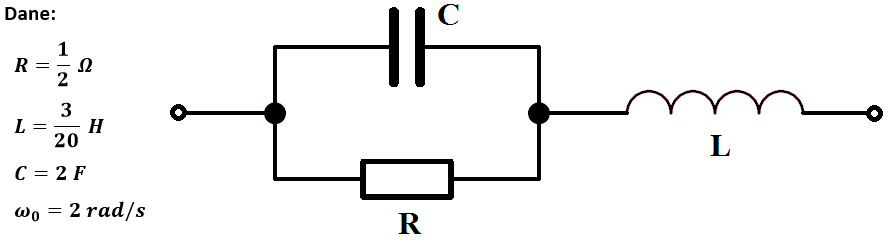
W pierwszej kolejności wstawmy w układ impedancje zgodnie ze wzorami.
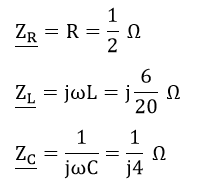
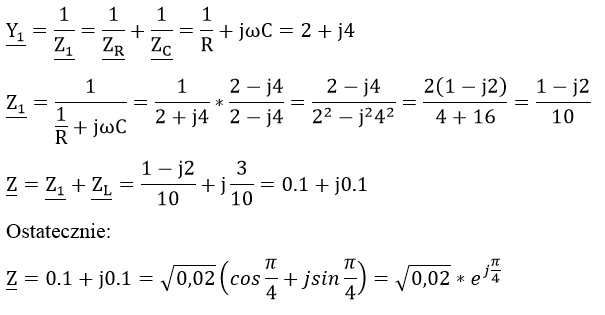
Odp. Zatem ostateczny wynik to: 0.1+j0.1 \Omega i postać wykładnicza: \sqrt{0.02}e^{j\frac{\pi}{4}}.
Przykład 2. (metoda symboliczna – Prawo Ohma)
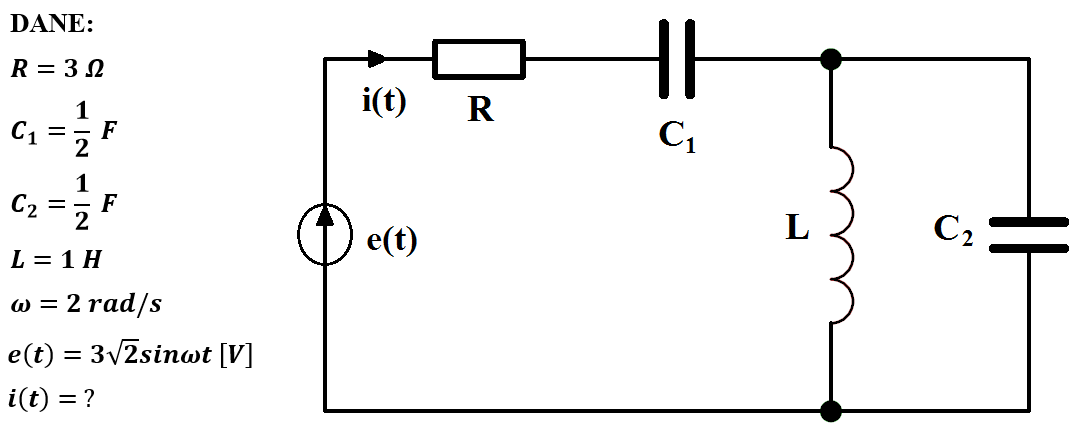
W danym poniżej schemacie obwodu panuje stan ustalony. Należy wyznaczyć prąd i(t).
Aby rozwiązać tego typu zadanie należy skorzystać z metody symbolicznej i Prawa Ohma. Napięcie mamy dane: e(t). Szukamy prąd i(t), zatem po zamianie na wartość zespoloną nasze Prawo Ohma przyjmie postać:
Prąd w metodzie symbolicznej to I, napięcie to E, natomiast Z jest impedancją, czyli oporem. Wniosek jest taki, że aby wyznaczyć przebieg prądu należy wyznaczyć impedancję, dzięki temu będziemy mogli podstawić pod wzór.
Zacznijmy od zamiany przebiegu czasowego napięcia na wartość zespoloną:
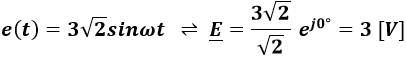
Następnie wyznaczmy impedancję:
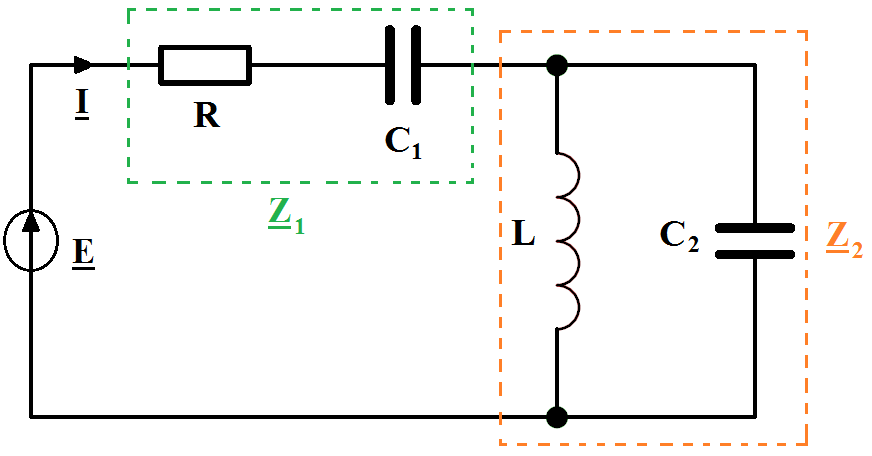
Impedancje łączymy szeregowo i wstawiamy wartości dane w zadaniu:
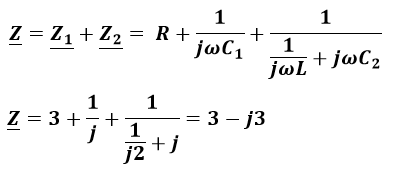
Teraz można już skorzystać z prawa Ohma, a wartość zespoloną prądu zamienić na przebieg czasowy:
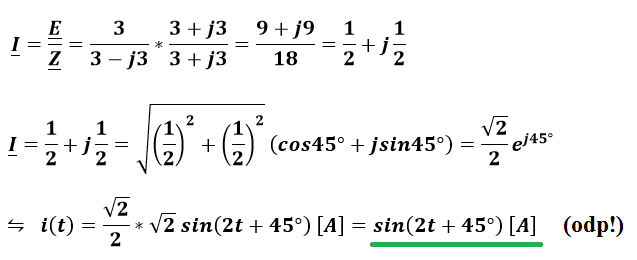
Zatem odpowiedzią jest wynik i(t)=sin(2t+45^o).